Shazam

Dieser Artikel ist eine Kopie des Artikel auf https://www.matheretter.de/wiki/shazam-uberblick.

Die gesamte Lesezeit aller Kapitel beträgt ca. 45 Minuten

Shazam Überblick

Lesezeit: 5 min

Ein Audio-Fingerabdruck ist eine digitale Zusammenfassung, die zum Identifizieren eines Audio-Samples oder zum schnellen Auffinden ähnlicher Objekte in einer Audiodatenbank verwendet werden kann. Wenn man beispielsweise jemandem ein Lied vorsummt, erstellt man einen Fingerabdruck, weil man für das Summen die Elemente aus der Musik herausholt/extrahiert, die man für wichtig hält (und wenn man ein guter Sänger ist, wird die andere Person das Lied wiedererkennen).

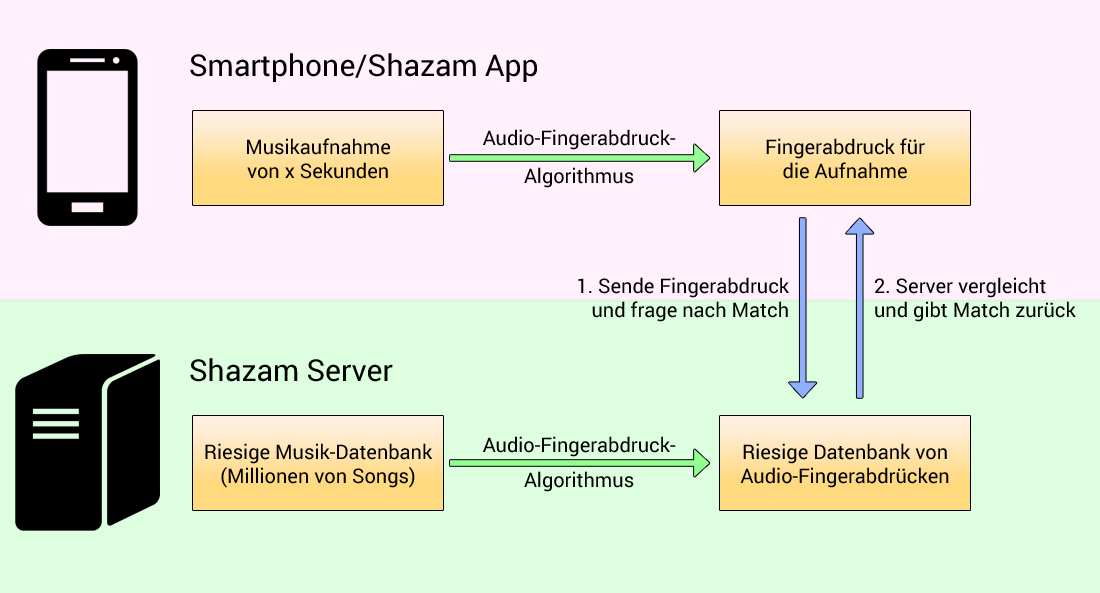
Bevor wir tiefer einsteigen, soll die folgende Abbildung die vereinfachte Architektur von Shazam zeigen. Dies ist jedoch nur eine Annahme, denn Shazam legt nicht alle notwendigen Informationen für das Verfahren offen. Siehe hierzu das Paper „An Industrial-Strength Audio Search Algorithm“ des Shazam-Mitbegründers Avery Li-Chun Wang aus dem Jahr 2003.

Auf der Serverseite:

Auf der Clientseite:

Die Schlüsselpunkte von Shazam sind:

Spektrogrammfilterung

Lesezeit: 12 min

Audio-Fingerabdrücke unterscheiden sich von standardmäßigen Computer-Fingerabdrücken wie SSHA oder MD5, da zwei verschiedene Dateien (in Bezug auf Bits), die die gleiche Musik enthalten, den gleichen Audio-Fingerabdruck haben müssen. Zum Beispiel muss ein Song in einem 256 kbit ACC-Format (iTunes) den gleichen Fingerabdruck ergeben wie in einem 256 kbit MP3 Format (Amazon) oder in einem 128 kbit WMA Format (Microsoft). Um dieses Problem zu lösen, verwenden Audio-Fingerabdruck-Algorithmen das Spektrogramm von Audiosignalen, um Fingerabdrücke zu extrahieren.

Spektrogramm erzeugen 

Wir hatten bereits gesagt, dass eine FFT angewendet werden muss, um ein Spektrogramm von einem digitalen Sound zu erzeugen. Für einen Fingerabdruck-Algorithmus benötigen wir eine gute Frequenzauflösung (z. B. 10,7 Hz), um 1. Spektrumlecks* zu reduzieren und 2. die wichtigsten Noten innerhalb des Songs herauszufiltern. Gleichzeitig müssen wir die Rechenzeit so weit wie möglich reduzieren und daher die kleinstmögliche Fenstergröße verwenden.

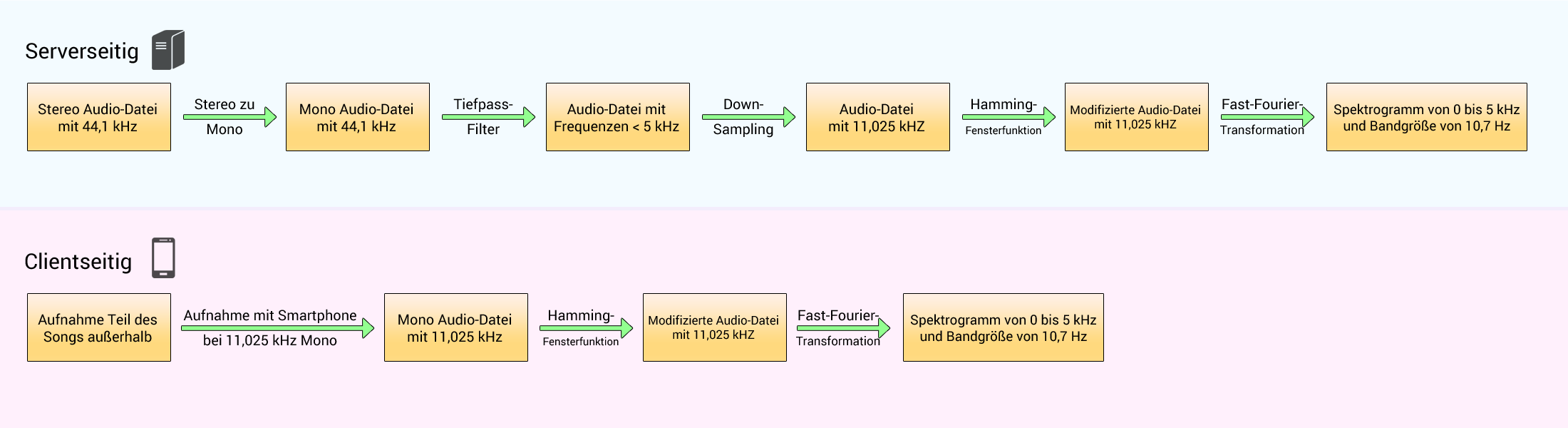
Im Paper von Shazam wird nicht erklärt, auf welche Weise man das Spektrogramm erhält, aber hier sei eine Möglichkeit gezeigt:

Auf der Serverseite (Shazam) muss der 44,1 kHz-gesampelte Sound (von CD, MP3 oder einem anderen Soundformat) von Stereo zu Mono übergehen. Wir können das tun, indem wir den Durchschnitt des linken und des rechten Lautsprechers nehmen. Vor dem Downsampling müssen wir die Frequenzen oberhalb von 5 kHz herausfiltern, um Aliasing zu vermeiden. Dann kann der Ton bei 11,025 kHz heruntergemischt (Downsampling) werden.

Auf der Clientseite (Smartphone) muss die Abtastrate des Mikrofons (Sampling rate), das den Ton aufzeichnet, bei 11,025 kHz liegen.

Dann müssen wir in beiden Fällen eine Fensterfunktion auf das Signal anwenden (wie ein Hamming 1024-Sample-Fenster, Grund hierfür siehe Kapitel Fensterfunktion) sowie die FFT für jede 1024 Samples. Auf diese Weise analysiert jede FFT 0,1 Sekunden Musik. Dies gibt uns ein Spektrogramm mit folgenden Eigenschaften:

Filtern 

An dieser Stelle haben wir das Spektrogramm des Songs. Da Shazam geräuschtolerant sein muss, werden nur die lautesten Töne beibehalten. Doch es ist noch nicht genug, nur die X stärksten Frequenzen alle 0,1 Sekunden beizubehalten. Hier sind einige Gründe:

Hier ist eine einfache Möglichkeit, nur starke Frequenzen beizubehalten und gleichzeitig die vorgenannten Probleme zu verringern:

Schritt 1 – Für jedes FFT-Ergebnis setzt man die 512 Bänder in 6 logarithmische Bänder:

Schritt 2 – Für jedes Band behält man nur das stärkste Band der Frequenzen.

Schritt 3 – Dann berechnet man den Durchschnittswert dieser 6 stärksten Bänder.

Schritt 4 – Man behält die Bänder (von den 6 Bändern), die sich über diesem Durchschnitt befinden (multipliziert mit einem Koeffizienten).

Der letzte Schritt ist äußerst wichtig, da folgende Fälle auftreten können:

Außerdem wollen wir keine schwache Frequenz in einem Band behalten, nur weil sie die stärkste innerhalb ihres Bandes ist.

Dieser Algorithmus hat jedoch eine Einschränkung. In den meisten Songs sind einige Teile sehr schwach, so zum Beispiel der Anfang oder das Ende eines Songs. Wenn man diese Teile analysiert, erhält man falsche starke Frequenzen, weil der Mittelwert (berechnet in Schritt 3) dieser Teile sehr niedrig ist. Um das zu vermeiden, kann man, anstatt den Mittelwert der 6 stärksten Bänder der aktuellen FFT zu nehmen (das entspricht nur 0,1 Sekunden des Songs), den Mittelwert der stärksten Bänder des gesamten Songs nehmen.

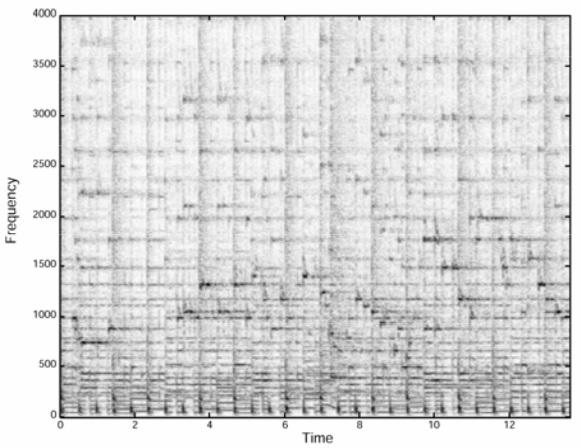
Fazit: Indem wir diesen Algorithmus benutzen, filtern wir das Spektrogramm des Songs und behalten die Frequenzspitzen (Peaks) im Spektrum bei, die die lautesten Noten repräsentieren. Um eine Vorstellung davon zu haben, was diese Filterung macht, sei nachstehend ein echtes Spektrogramm eines 14-Sekunden-Songs gezeigt.

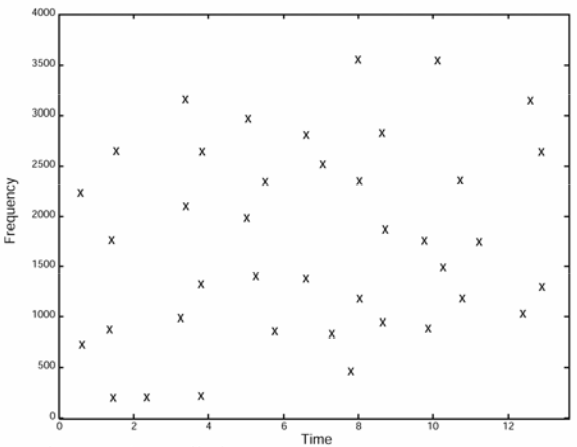
Diese Abbildung stammt aus dem Shazam-Paper. In diesem Spektrogramm kann man sehen, dass einige Frequenzen stärker sind als andere. Wenn man den vorgenannten Algorithmus auf das Spektrogramm anwendet, erhält man Folgendes:

Diese Abbildung (siehe auch Shazam-Paper) zeigt ein gefiltertes Spektrogramm. Nur die stärksten Frequenzen aus der vorherigen Abbildung werden beibehalten. Einige Teile des Songs haben nach der Filterung keine Frequenz mehr (zum Beispiel zwischen 4 und 4,5 Sekunden).

Die Anzahl der Frequenzen im gefilterten Spektrogramm hängt von dem Koeffizienten ab, der bei Schritt 4 mit dem Mittelwert verwendet wurde. Sie hängen auch von der Anzahl der Bänder ab, die man verwendet (wir haben 6 Bänder verwendet, aber wir hätten auch eine andere Zahl wählen können).

An dieser Stelle ist die Intensität der Frequenzen nutzlos. Daher kann dieses Spektrogramm als zweispaltige Tabelle modelliert werden, bei der:

Dieses gefilterte Spektrogramm ist nicht der endgültige Audio-Fingerabdruck, aber es ist bereits ein großer Teil davon. Im nächsten Kapitel erfahren wir mehr darüber.

Hinweis: Wir haben gerade einen einfachen Algorithmus kennengelernt, um das Spektrogramm zu filtern. Ein besserer Ansatz könnte darin bestehen, ein logarithmisches Gleitfenster zu verwenden und nur die stärksten Frequenzen über dem Mittelwert + der Standardabweichung (multipliziert mit einem Koeffizienten) eines sich bewegenden Teils des Songs zu behalten. Dieser Ansatz ist jedoch schwieriger zu erklären.

Fingerabdrücke speichern

Lesezeit: 15 min

Wir haben im vorigen Kapitel ein gefiltertes Spektrogramm für einen Songs erstellt. Wie können wir dieses Spektrogramm nun effizient speichern und nutzen? Darin liegt die eigentliche Stärke von Shazam. Um das Problem zu verstehen, gehen wir von einer vereinfachten Situation aus: Wir suchen nach einem Song, indem wir direkt sein gefiltertes Spektrogramm verwenden.

Einfacher Suchansatz 

Vorbereitender Schritt: Wir erstellen eine Datenbank mit gefilterten Spektrogrammen für alle Songs auf unserem Computer.

Schritt 1: Wir nehmen einen 10-Sekunden-Teil eines Songs auf, der gerade auf dem Fernseher gespielt wird, und übertragen ihn auf den Computer.

Schritt 2: Wir berechnen das gefilterte Spektrogramm dieser Aufnahme.

Schritt 3: Wir vergleichen dieses "kleine" Spektrogramm mit dem "vollen" Spektrogramm jedes einzelnen Songs.

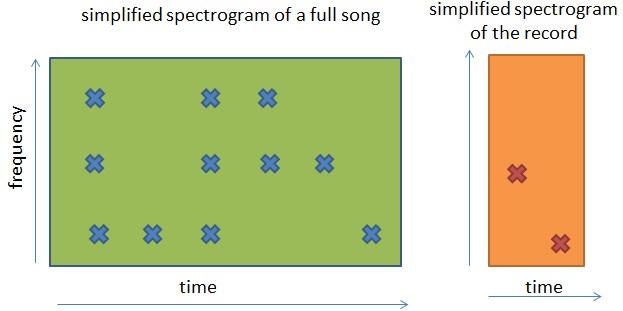
Doch wie können wir ein 10-Sekunden-Spektrogramm mit dem Spektrogramm eines 180-Sekunden-Songs vergleichen? Hier ist eine visuelle Erklärung dessen, was zu tun ist:

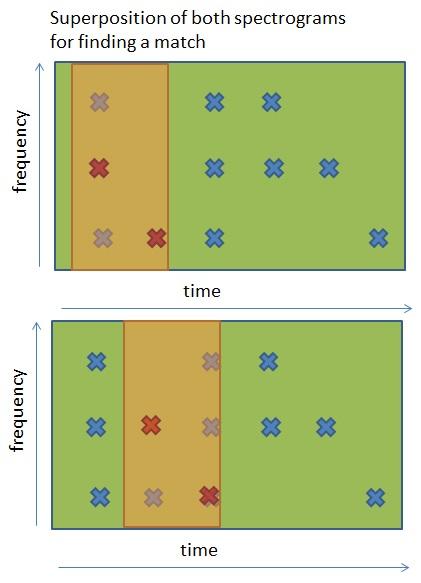
Visuell müssen wir das kleine Spektrogramm nehmen und mit dem Spektrogramm des vollständigen Songs Stück für Stück überlagern, um herauszufinden, ob das kleine Spektrogramm mit einem Teil des vollständigen Spektrogramms übereinstimmt.

Wir müssen dies für jeden Song tun, der sich in unserer Datenbank befindet, bis wir eine perfekte Übereinstimmung gefunden haben.

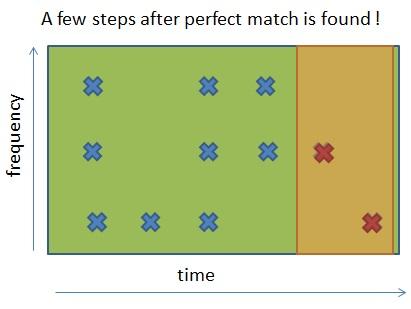
In der letzten Abbildung erkennen wir eine perfekte Übereinstimmung zwischen der Aufnahme und dem Ende des Songs. Sollten wir keinen Match haben, so müssten wir die Aufnahme mit einem anderen Song vergleichen, bis wir eine Übereinstimmung finden. Wenn wir keine perfekte Übereinstimmung finden, können wir zumindest die beste Übereinstimmung wählen, die sich beim Vergleich mit allen Songs ergibt, hierzu würden wir einen Schwellenwert benutzen. Als Beispiel: Wenn die beste Übereinstimmung zwischen Aufnahme und Originalsong eine 90%-ige Ähnlichkeit aufweist, können wir annehmen, dass es der richtige Song ist, weil die 10 % Abweichung wahrscheinlich auf externes Rauschen zurückzuführen sind.

Obwohl dieser einfache Ansatz gut funktioniert, erfordert er sehr viel Rechenzeit. Man muss sämtliche Möglichkeiten der Übereinstimmung zwischen der 10-Sekunden-Aufnahme und jedem einzelnen Song in der Sammlung berechnen. Angenommen, die Musik enthält durchschnittlich 3 Spitzenfrequenzen (Peaks) je 0,1 Sekunden, dann hätte das gefilterte Spektrogramm der 10-Sekunden-Aufnahme 300 Zeit-Frequenz-Punkte. Um den richtigen Song zu finden, würden wir im schlimmsten Fall 300·300·30·S = 2 700 000 · S Operationen benötigen, wobei S die Anzahl der Sekunden der Musik in unserer Sammlung meint. Wenn wir 30 000 Songs haben (ca. 7·10⁶ Sekunden Musik), kann dieser Suchprozess sehr lange dauern. Und für Shazam wäre dies noch wesentlich aufwändiger, da dort ca. 40 Millionen Songs gespeichert sind (diese Zahl ist nur eine Vermutung, die konkrete Datenbankgröße ist nicht öffentlich).

Fragt sich nun, wie macht Shazam das so schnell und effizient?

Zielzonen 

Anstatt jeden Punkt einzeln zu vergleichen, sucht man nach mehreren Punkten gleichzeitig. Im Shazam-Paper wird diese Gruppe von Punkten als Zielzone bezeichnet. Das Paper von Shazam erklärt jedoch nicht, wie man diese Zielzonen erzeugt. Trotzdem sei im Folgenden eine Möglichkeit hierfür beschrieben. Damit es leichter zu verstehen ist, werden wir die Größe der Zielzone an 5 Frequenz-Zeitpunkten festlegen.

Um sicherzustellen, dass sowohl die Aufnahme als auch der vollständige Song die gleichen Zielzonen erzeugen, benötigt man eine Ordnungsrelation zwischen den Zeit-Frequenz-Punkten in einem gefilterten Spektrogramm. Hier ist eine solche Ordnungsrelation:

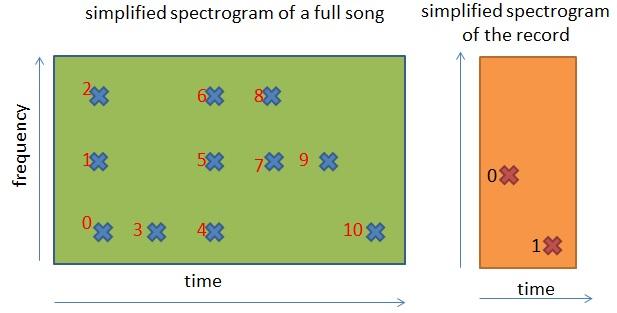
Wenn man diese Reihenfolge auf das vereinfachte Spektrogramm anwendet, das wir oben gezeigt hatten, dann erhält man Folgendes:

In dieser Abbildung haben wir alle Zeit-Frequenz-Punkte auf Grundlage der Ordnungsrelation markiert. Zum Beispiel:

Da die Spektrogramme nun innerlich geordnet werden können, können wir dieselben Zielzonen auf verschiedenen Spektrogrammen erzeugen. Hierfür nutzen wir folgende Regel: „Um Zielzonen in einem Spektrogramm zu erzeugen, muss man für jeden Zeit-Frequenz-Punkt eine Gruppe aus diesem Punkt und aus dessen 4 darauffolgenden Punkten erstellen“. Wir erhalten damit ungefähr die gleiche Anzahl an Zielzonen wie Anzahl an Punkten. Bei den Songs und bei der Aufnahme wird diese Regel gleichermaßen angewendet.

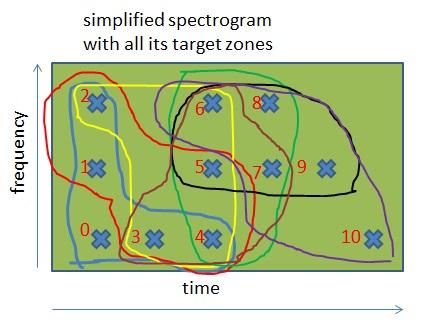
In diesem vereinfachten Spektrogramm kann man die verschiedenen Zielzonen sehen, die vom vorherigen Algorithmus generiert wurden. Da die Zielgröße 5 ist, gehören die meisten Punkte zu 5 Zielzonen (mit Ausnahme der Punkte am Anfang und Ende des Spektrogramms).

Hinweis: Zunächst war es für mich nicht verständlich, warum wir für die Aufnahme so viele Zielzonen berechnen müssen. Wir könnten Zielzonen doch beispielsweise mit solch einer Regel erzeugen: „Für jeden Punkt, dessen Label ein Vielfaches von 5 ist, muss man eine Gruppe erstellen, die aus dieser Frequenz und den 4 Frequenzen danach besteht“. Mit dieser Regel würde die Anzahl der Zielzonen um den Faktor 5 reduziert werden - und damit auch die erforderliche Suchzeit (diese wird im nächsten Kapitel erklärt). Der einzige mögliche Grund ist, dass die Berechnung aller möglichen Zonen sowohl für die Aufnahme als auch für den Song die Rauschtoleranz stark erhöht.

Adressgenerierung 

Wir haben jetzt mehrere Zielzonen, was machen wir als nächstes? Wir erstellen für jeden Punkt eine Adresse basierend auf diesen Zielzonen. Um diese Adressen zu erstellen, benötigen wir zusätzlich einen Ankerpunkt pro Zielzone. Auch hier erklärt das Shazam-Paper nicht, wie das geht. Stellen wir uns also vor, dass dieser Ankerpunkt der 3. Punkt vor der Zielzone ist. Der Anker kann beliebig sein, solange die Art und Weise wie er erzeugt wird, reproduzierbar ist (was dank unserer Ordnungsrelation möglich ist).

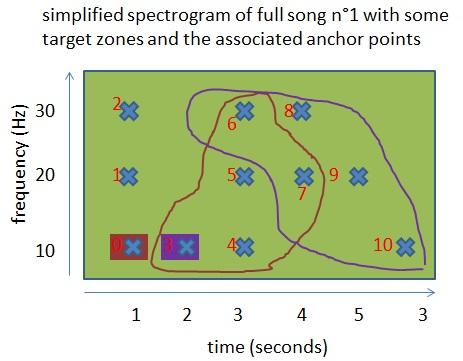
In dieser Abbildung sind 2 Zielzonen mit ihren Ankerpunkten gezeichnet. Konzentrieren wir uns auf die violette Zielzone. Die von Shazam vorgeschlagene Adressformel folgt einem:

["Frequenz des Ankers"; "Frequenz des Punktes"; "Deltazeit zwischen Anker und Punkt"].

Für die violette Zielzone:

Beide Punkte erscheinen auch in der braunen Zielzone, ihre Adressen mit dieser Zielzone sind [10; 30; 2] für Punkt 6 und [10; 20; 3] für Punkt 7.

Wir haben über „Adressen“ gesprochen. Das impliziert, dass diese Adressen mit etwas verknüpft sind. Im Falle der vollen Songs (also nur auf der Serverseite) sind diese Adressen mit dem folgenden Paar verbunden: ["absolute Zeit des Ankers im Song"; "Song-ID"]. In unserem einfachen Beispiel mit den 2 vorherigen Punkten haben wir dann das folgende Ergebnis:

[10; 30; 1] → [2; 1]

[10; 30; 2] → [2; 1]

[10; 30; 2] → [1; 1]

[10; 30; 3] → [1; 1]

Wenn man die gleiche Logik für alle Punkte aller Zielzonen aller Song-Spektrogramme anwendet, erhält man eine sehr große Tabelle mit zwei Spalten:

Diese Tabelle ist die Audio-Fingerabdruck-Datenbank von Shazam. Wenn ein Song durchschnittlich 30 Spitzenfrequenzen pro Sekunde enthält und die Zielzone 5 ist, beträgt die Größe dieser Tabelle 5·30·S, wobei S die Anzahl der Sekunden der Musiksammlung ist.

Erinnern wir uns, wir hatten eine FFT mit 1024 Samples verwendet, das heißt, dass es nur 512 mögliche Frequenzwerte gibt. Diese Frequenzen können in 9 Bits kodiert werden ("⁹ = 512). Unter der Annahme, dass die Deltazeit in Millisekunden liegt, wird sie niemals über 16 Sekunden liegen, da dies einen Song mit einem 16-Sekunden-Part ohne Musik (oder sehr niedrigen Sound) bedeuten würde. So kann die Deltazeit in 14 Bits kodiert werden (2¹⁴ = 16 384). Die Adresse kann in einer 32-Bit-Ganzzahl (Integer) codiert werden:

Unter Verwendung derselben Logik kann das Paar ("Zeit des Ankers"; "Song-ID") in einer &4-Bit-Ganzzahl (Integer) codiert werden (§2 Bit für jeden Teil).

Die Fingerabdruck-Tabelle kann als ein einfaches Array von 64-Bit-Ganzzahlen implementiert werden, wobei:

Mit anderen Worten: Wir haben die Fingerabdruck-Tabelle in eine invertierte Suche umgewandelt, die einen Suchvorgang in O(1) ermöglicht, also eine sehr effektive Suchzeit hat.

Hinweis: Sicher hast du dich gefragt, warum wir den Ankerpunkt nicht innerhalb der Zielzone gewählt haben. Wir hätten als Ankerpunkt zum Beispiel den ersten Punkt der Zielzone wählen können. Wenn wir das jedoch getan hätten, hätten wir viele Adressen der Form [Frequenz-Anker; Frequenz-Anker; 0] erzeugt. Dadurch wären viele Paare ["Ankerzeit"; "Song-ID"] mit der Adresse [Y, Y, 0] entstanden, wobei Y die Häufigkeit (zwischen 0 und 511) angibt. Mit anderen Worten, das Nachschlagen wäre verzerrt gewesen.

Fingerabdrücke suchen und bewerten

Lesezeit: 5 min

Wir haben jetzt eine praktische Datenstruktur auf der Serverseite, wie können wir sie nun verwenden?

Suche 

Um eine Suche durchzuführen, wird die Erzeugung des Fingerabdrucks direkt für die aufgenommene Audiodatei ausgeführt (auf dem Smartphone), sodass eine Adress-/Wert-Struktur erzeugt wird, die sich geringfügig auf Seiten des Wertes unterscheidet:

["Frequenz des Ankers"; "Frequenz des Punktes"; "Deltazeit zwischen dem Anker und dem Punkt"] → ["absolute Zeit des Ankers in Aufnahme"].

Diese Daten werden dann an den Shazam-Server gesendet. Wenn wir annehmen, dass 300 Zeit-Frequenz-Punkte im gefilterten Spektrogramm des 10-Sekunden-Aufnahme vorhanden sind und eine Zielzone aus 5 Punkten besteht, dann bedeutet das, dass ungefähr 1500 Daten an Shazam gesendet werden.

Jede Adresse aus der Aufnahme wird verwendet, um in der Fingerabdruck-Datenbank nach den zugehörigen Paaren ["absolute Zeit des Ankers im Song"; "Song-ID"] zu suchen. In Bezug auf die Zeit-Komplexität (unter der Annahme, dass die Fingerabdruck-Datenbank innerhalb des Speichers ist) ist die Suche proportional zur Anzahl der an Shazam gesendeten Adressen (in unserem Fall 1500). Diese Suche ergibt eine große Anzahl an Paaren, sagen wir für den Rest des Artikels, dass sie M Paare zurückgibt.

Obwohl M riesig ist, ist es viel niedriger als die Anzahl der Noten (Zeit-Frequenz-Punkte) aller Songs zusammen. Die wahre Stärke dieser Suche besteht darin, dass wir nicht suchen, ob eine Note in einem Song existiert, sondern ob 2 Noten getrennt von Deltazeit Sekunden im Song vorhanden sind. Am Ende dieses Kapitels werden wir noch mehr über diese Zeit-Komplexität sprechen.

Ergebnisfilterung 

Obwohl es in dem Shazam-Paper nicht erwähnt wird, ist anzunehmen, dass der nächste Schritt die Filterung der M Suchergebnisse ist, indem nur die Paare der Songs beibehalten werden, die eine Mindestzahl von Zielzonen gemeinsam mit der Aufzeichnung haben.

Lasst uns zum Beispiel annehmen, dass unsere Suche Folgendes ergibt:

Unsere 10-Sekunden-Aufnahme hat (ungefähr) 300 Zielzonen. Im besten Fall:

Wir werden nur die Paare der Songs 13 und 25 für das Ergebnis behalten. Obwohl die Songs 1, 2, 5 und 8 mehrere Paare mit der Aufnahme gemeinsam haben, bildet keines von ihnen zusammen mit der Aufnahme mindestens eine Zielzone (von 5 Punkten). Dieser Schritt kann viele falsche Ergebnisse entfernen, da die Fingerabdruck-Datenbank von Shazam viele Paare für die gleiche Adresse hat und man leicht mit Paaren an der gleichen Adresse enden könnte, die nicht zur selben Zielzone gehören. Wenn du den Grund nicht verstehst, sieh dir das letzte Bild des vorherigen Kapitels an: Die [10; 30; 2]-Adresse wird von zwei Zeit-Frequenz-Punkten verwendet, die nicht zur selben Zielzone gehören. Wenn die Aufnahme auch eine [10; 30; 2] enthält, wird (mindestens) eines der beiden Paare im Ergebnis in diesem Schritt herausgefiltert.

Dieser Schritt kann in O(M) mit Hilfe einer Hash-Tabelle ausgeführt werden, deren Key das Paar ["Song-ID"; "absolute Zeit des Ankers im Song"] ist sowie der Häufigkeit, die es im Ergebnis erscheint:

*Die Idee ist, nach der Zielzone zu suchen, die durch einen Ankerpunkt in einem Song erzeugt wird. Dieser Ankerpunkt kann durch die Song-ID, zu dem er gehört, und durch die absolute Zeit definiert werden. Wir haben hier eine Annäherung vorgenommen, weil man in einem Song mehrere Ankerpunkte gleichzeitig haben kann. Da es sich um ein gefiltertes Spektrogramm handelt, haben wir nicht viele Ankerpunkte gleichzeitig. Jedoch wird der Key ["Song-ID"; "absolute Zeit des Ankers im Song"] alle Zielzonen erfassen, die von diesen Zielpunkten erzeugt werden.

Hinweis: Wir haben in diesem Algorithmus zwei Hashtabellen verwendet. Wenn du nicht weißt, wie das funktioniert, denk es dir einfach als einen sehr effizienten Weg, Daten zu speichern und abzurufen. Wenn du mehr wissen willst, kannst du den Artikel über die HashMap in Java (Englisch) lesen, der eine effiziente Hash-Tabelle ist.

Zeitkohärenz 

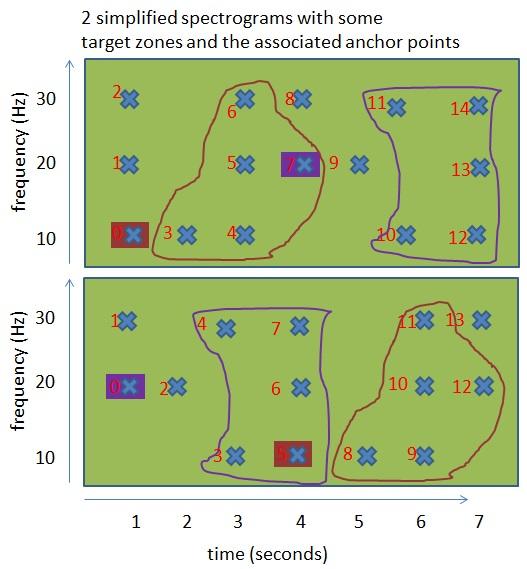
An dieser Stelle haben wir Songs gefunden, die wirklich nah an der Aufnahme sind. Aber wir müssen immer noch die Zeitkohärenz (Zusammenhang über die Zeit) zwischen den Noten der Aufnahme und diesen Songs verifizieren. Hier ist der Grund dafür:

In dieser Abbildung haben wir 2 Zielzonen, die zu 2 verschiedenen Songs gehören. Wenn wir die Zeitkohärenz nicht beachten, würden diese Zielzonen die Übereinstimmungsraten zwischen den zwei Songs erhöhen, obwohl sie nicht gleich klingen, da die Noten in diesen Zielzonen nicht in derselben Reihenfolge gespielt werden.

In diesem letzten Schritt geht es um die zeitliche Reihenfolge. Die Idee ist:

Jetzt, wo wir eine gute Vorstellung vom Algorithmus bekommen haben, schauen wir uns an, wie wir dies technisch umsetzen können. An dieser Stelle haben wir für eine Liste von Adressen/Werten:

["Frequenz des Ankers"; "Frequenz des Punktes"; "Deltazeit zwischen dem Anker und dem Punkt"] → ["absolute Zeit des Ankers und der Aufnahme"].

Und wir haben für jeden Song eine Liste von Adressen/Werten (in der Hash-Tabelle des vorherigen Schritts gespeichert):

["Frequenz des Ankers"; "Frequenz des Punktes"; "Deltazeit zwischen dem Anker und dem Punkt"] → ["absolute Zeit des Ankers im Song"; "Song-ID"].

Der folgende Prozess muss für alle verbleibenden Songs durchgeführt werden:

Von allen Songs behalten wir den Song mit den meisten zeitkohärenten Noten. Wenn diese Kohärenz über "der Anzahl der Noten in der Aufnahme" * "ein Koeffizient" liegt, dann ist dieser Song der richtige.

Wir müssen dann nur noch nach den Metadaten des Songs ("Künstlername", "Songname", "iTunes URL", "Amazon URL", ...) mit der Song-ID suchen und das Ergebnis an den Nutzer zurückgeben.

Ein Wort über Komplexität 

Diese Suche ist wirklich komplizierter als die einfache Suche, die wir zuerst kennengelernt hatten. Mal sehen, ob uns die Komplexität einen Vorteil bringt. Die erweiterte Suche ist ein schrittweiser Ansatz, der die Komplexität bei jedem Schritt reduziert.

Damit es besser zu verstehen ist, führen wir noch mal alle getroffenen Annahmen bzw. Entscheidungen auf, die wir gemacht hatten. Zudem kommen neue Annahmen hinzu, um das Problem zu vereinfachen:

Der erste Schritt zur Suche erfordert nur 5 · 300 unitäre Suchen.

Die Größe des Ergebnisses M ist die Summe des Ergebnisses der 5 · 300 unitären Suchen:

M = (5 · 300) ·(S · 30 · 5 · 300) / (512 · 512 · 2)

Der zweite Schritt ist die Ergebnisfilterung, sie kann in M-Operationen erfolgen. Am Ende dieses Schrittes sind N Noten verteilt in Z Songs. Ohne eine statistische Analyse der Musiksammlung ist es unmöglich, den Wert von N und Z zu erhalten. N sollte niedriger sein als M, und Z sollte nur ein paar Songs darstellen, sogar bei einer riesigen Songdatenbank wie der von Shazam.

Der letzte Schritt ist die Analyse der Zeitkohärenz der Z Songs. Wir nehmen an, dass jeder Song ungefähr die gleiche Menge an Noten hat: N/Z. Im schlimmsten Fall (eine Aufnahme von einem Song, der nur eine Note enthält, die kontinuierlich gespielt wird), ist die Komplexität einer Analyse (%·300)·(N/Z).

Die Kosten der Z Songs betragen: 5·300·N.

Da N<<M, entsprechen die tatsächlichen Kosten dieser Suche:

M = (300 · 300 · 30 · S) · (5 · 5) / (512 · 512 · 2) = 67500000 / 524288 · S = 128,75 · S

Zur Erinnerung: Die Kosten der einfachen Suche waren:

300 · 300 · 30 · S = 2 700 000 · S

Diese neue Suche ist ca. 20 000 mal schneller!

Hinweis: Die wahre Komplexität hängt von der Verteilung der Frequenzen innerhalb der Songsammlung ab, aber diese einfache Kalkulation gibt uns eine gute Vorstellung von der tatsächlichen Berechnung.

Verbesserungen 

Das Shazam-Paper stammt aus dem Jahr 2003 und die damit verbundenen Forschungen sind noch älter. Im Jahr 2003 wurden 64-Bit-Prozessoren auf dem Mainstream-Markt veröffentlicht.

Anstatt einen Ankerpunkt pro Zielzone zu verwenden, wie es das Papier vorschlägt (wegen der begrenzten Größe einer 32-Bit-Ganzzahl), könnte man 3 Ankerpunkte verwenden (z. B. die § Punkte unmittelbar vor der Zielzone) und die Adresse eines Punktes in der Zielzone in einer 64-Bit-Ganzzahl speichern. Dies würde die Suchzeit dramatisch verbessern.

In der Tat würde die Suche 4 Noten in einem Song finden, getrennt von delta_time1, delta_time2 und delta_time3 (in Sekunden), wodurch die Anzahl der Ergebnisse M sehr (sehr) niedriger wäre als die, die wir gerade berechnet haben.

Ein großer Vorteil dieser Fingerabdrucksuche ist übrigens ihre hohe Skalierbarkeit:

Kompromisse 

Eine weitere interessante Diskussion ist die Rauschtoleranz bzw. Rauschrobustheit dieses Algorithmus. Hierüber könnten wir einen eigenen umfangreichen Artikel schreiben, doch an dieser Stelle es ist besser, nur ein paar Worte darüber zu verlieren.

Wenn du aufmerksam gelesen hast, hast du bemerkt, dass wir viele Schwellenwerte, Koeffizienten und feste Werte verwendet haben (wie die Abtastrate, die Dauer einer Aufnahme etc.). Wir haben auch viele Algorithmen gewählt (um ein Spektrogramm zu filtern, um ein Spektrogramm zu erzeugen usw.). Sie alle haben einen Einfluss auf den Rauschwiderstand und die Zeitkomplexität. Die wahre Herausforderung besteht darin, die richtigen Werte und Algorithmen zu finden, die:

maximieren.

Fazit

Lesezeit: 4 min

Im besten Fall verstehst du jetzt wie Shazam funktioniert. Der Autor hat viel Zeit benötigt, um die verschiedenen Themen dieses Artikels zu verstehen. Dieser Artikel macht dich vielleicht nicht zu einem Experten, doch du hast zumindest ein sehr gutes Bild von den Prozessen, die hinter Shazam stecken. Denke daran, dass Shazam nur eine von mehreren möglichen Implementierungen für Audio-Fingerabdrücke ist.

Du solltest jetzt theoretisch in der Lage sein, dein eigenes Shazam zu programmieren. Du kannst dir diesen sehr guten Artikel ansehen, der sich mehr darauf konzentriert, wie man ein vereinfachtes Shazam in Java programmiert, und weniger auf die dahinter stehenden Konzepte. Du kannst auch „Robust Landmark-Based Audio Fingerprinting“ lesen, dort geht es um eine MatLab-Implementierung von Shazam. Und selbstverständlich kannst du das Paper von Shazam-Mitbegründer Avery Li-Chun Wang hier selbst durchlesen.

Die Welt des Musikberechnens (Music Computing) ist ein sehr interessantes Feld mit praktischen Algorithmen, die wir jeden Tag benutzen, ohne es zu wissen. Obwohl Shazam nicht leicht zu verstehen ist, ist es einfacher als:

Falls du Interesse hast: Es gibt einen jährlichen Wettbewerb zwischen Forschern zu diesen Themen. Er heißt MIREX-Wettbewerb. Die Algorithmen der einzelnen Teilnehmer werden dort auch veröffentlicht.

Der Autor hat in den letzten 3 Jahren ungefähr 200 Stunden damit verbracht, die Signalverarbeitungskonzepte und die Mathematik dahinter zu verstehen, er hat einen eigenen Shazam-Prototypen programmiert, Wangs Paper vollständig verstanden und sich die Prozesse erarbeitet, die das Paper nicht erklärt. Sein Beweggrund: „Ich habe diesen Artikel geschrieben, weil ich nie einen Artikel gefunden habe, der Shazam wirklich erklärt und ich wünschte, ich hätte einen Artikel im Jahr 2012 finden können, als ich mit diesem Nebenprojekt begann.“

Falls du einen Fehler im Artikel findest, so trage ihn bitte hier ein: Hinweise zum Artikel: Wie funktioniert Shazam

Fragen zum Artikel? Dann stelle sie bitte in der Mathelounge (Stichwort "shazam").